Deciding Suitability of Empirical formulas for Hydraulic calculations

yogendra borse

In calculating discharge with Inglis/Dickens formulas the Constant values are given irrespective of terrain characteristics which literally means that the velocity or discharge is not affected by the terrain. This is quite unexpected,  hence the constant values must differ as per catchment area slope. Steeper the slope of catchment lesser the time of concentration hence higher the constant value.

 Earlier graphs showing the relation between the slope of catchment and coefficient for empirical formula were given but recently this method is not used by anybody resulting in calculations, which have no consideration for catchment slope.

Can velocity of water flow through river in region shown below 2 images can match?

Image -1  Hilly Terrain

Image-2 Flat terrain 

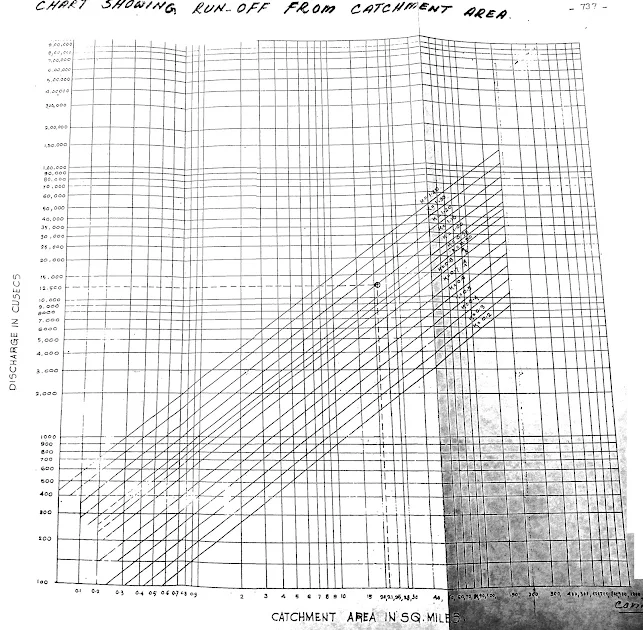
R.D.S.O. have developed some charts showing runoff from catchment areas.

Steps to calculate Discharge is as follows

Step 1)  From map Estimate 2 year 1 hour rainfall intensity from Map

For Akola area its 2 years 1 hour Rainfall is 2.4

Step 2) Search Catchment area zone on map

From Map it is seen that catchment area lies in zone number II

Step 3) From map Estimate multiplying factor for 50 year 1 hour rainfall intensity

Ratio of n Year 1 hour rainfall to 2 year 1 hour rainfall
Zone	5	10	20	25	30	40	50
I	1.2	1.38	1.54	1.62	1.65	1.73	1.85
II	1.26	1.46	1.74	1.84	1.9	2.04	2.17
III	1.31	1.6	2.03	2.14	2.27	2.52	2.64
IV	1.19	1.32	1.52	1.58	1.61	1.72	1.79

From Table Multiplying factor for getting ' 50 year' 1 hour rainfall is 1.85

Therefor '50 years, 1 hour rainfall over the catchment = 2.4 x 2.1 = 5.04

Step 4) Calculate Statistical slope of catchment area.

Statistical slope = ∑(Li Hi)/A

L = Length of successive contours from the boundary of catchment area to the other in miles to be measured on toposheets.

H = Catchment area in sq.miles

SR.No.	Value of Contour (ft)	Length pf contour lines (miles)
L1	1000	4.8
L2	1050	6.8
L3	1100	6.6
L4	1150	6.2
L5	1200	6
L6	1250	7.4
L7	1300	9.1
L8	1350	9.5
L9	1400	10.1
L10	1450	9.6
L11	1500	9
L12	1550	10
L13	1600	10.2
L14	1650	9.8
L15	1700	3
L16	1750	1.8
L17	1800	1.9
L18	1850	1.7
L19	1900	1.2
L20	1950	0.5
L21	2000	0.3

∑ Li = 125.5 miles

h X ∑ Li = 125.5 X 50 = 6275 

(h X ∑ Li)/2 = 6275/2 = 3137.5

(h X ∑ Li)/2A = 3137.5/21 = 149.404 ft/mile

Now 5280 ft = 1 mile 

hence % slope of catchment = 149.404 X 100 / 52.80 = 2.83 %

Step 5) Obtain Value of 'K' from Graph

Table showing 'K' values for different rainfalls and statistical slopes
50 Year 1 hour rainfall	Hilly slope 10% and above	Rough hilly 5% - 10%	Rolling 2% - 5%	Flat to Rolling 1.2%	Flat to Rolling 0.1%
2.5	-	-	0.8	0.3	0.15
3	0.92	0.9	0.85	0.5	0.2
3.5	0.93	0.92	0.9	0.6	0.25
4	0.95	0.94	0.92	0.7	0.3
4.8	1.1	0.96	0.95	0.9	0.35
5	1.2	1.06	1	0.95	0.4
5.5	1.3	1.28	1.1	1	-
6	1.3	1.32	1.15	-	-
6.5	1.34	-	-	-	-

For Rainfall intensity = 5.04 and Catchment slope = 2.83, K = 1.1

Step 6) Calculate Discharge from catchment area

catchment area = 21 sq.miles for  K = 0.91

Discharge = 12500 cusecs

Inglis Discharge = 29400 cusecs

Modified Inglis = 16000 cusecs

From Following graph Dickens constant C = 1300 hence

Dickens Discharge = 12740 Cusecs

Hence Most suitable formula for area under consideration is Dickens formula.